Today, I have mostly been breeding robots…
Back in my undergrad days, I learnt about “genetic algorithms”. The basic idea is that rather than designing a computer program yourself, you allow one to evolve: the equivalent of natural section. I’ve taken advantage of the break between Christmas and New Year to experiment with this; I’m trying to get robots to find their way through a maze. Just to clarify, this is all virtual: I’m writing programs on my computer, rather than building things out of Lego.
To be more precise, it’s the programs that are breeding, rather than the robots themselves. In fact, you can think of it as just one robot that runs different programs in turn. Each program is a list of 100 commands, and each command has 4 possible values (up/down/left/right), corresponding to directions in the maze. For instance, a program might go like this:
1. Move up.
2. Move left.
3. Move left.
4. Move down.
5. Move right.
etc.
I start out with 50 of these programs, which are randomly generated. My initial maze looks like this:
The green square at the bottom is the start, and the green square at the top is the exit. “Maze” is a bit of an exaggeration here, since there aren’t any walls in the middle! However, here’s an example of a random program:
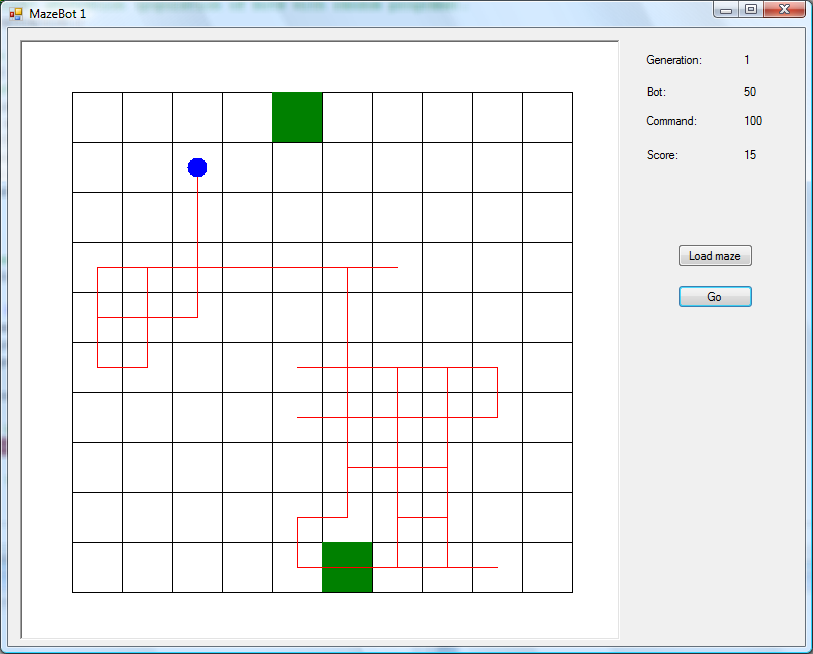
The blue dot is the robot, and the red line is the path it’s followed. As you can see, it’s just wandered back and forth, bouncing off the outer walls and going round in circles, and didn’t actually get as far as the exit. So, there’s definitely room for improvement here. (One side-effect of the random approach is that I’ve found a couple of robots drawing swastikas in the maze, which is slightly embarrassing!)
After the robot finishes running each program, I give it a score. If it’s reached the exit, it earns one point for each “spare” command that’s left. (For instance, if it got there on its 80th move, it would earn 20 points.) If it doesn’t reach the exit, it loses a point for each square that separates it from the exit. (This assumes that it could take the shortest possible route, and that there aren’t any obstacles in the way. In the example above, the robot is 3 squares away from the exit.) In a 10×10 maze, the furthest you can get from the exit is 18 squares (assuming that you’re in the opposite corner), which means that the lowest possible score is -18. So, I add 18 points to every score, which means they’ll never be negative. It doesn’t really matter, since it’s just the relative order that’s important, but it seems neater this way. This explains why the robot above got 15 points.
The next step is to choose “parents” for the next generation. Every robot (program) has a chance of being selected, but I skew the odds in favour of the bots that did better in the maze. This is the “weighted roulette wheel” approach. Imagine a normal roulette wheel, but then make some of the sections wider than others: this way, when the ball bounces around, it’s more likely to land on certain numbers.
In this case, I created an intermediate population. I sorted the bots from the first generation based on their scores, then copied each one into the intermediate list. The one at the bottom only gets 1 copy, then the one above that gets 2 copies, etc. In mathematical terms, that means that for n bots in the first generation, there will be 1+2+…+(n-1)+n bots in the intermediate population. There’s a convenient formula here: Sigma (1:n) = n(n+1)/2. (Sorry for not using MathML to format that nicely.) So, with 50 bots in the first generation, there are 1275 bots in the intermediate population.
So, I choose 25 pairs of bots from the intermediate population; due to the extra copies, one pair may actually be two copies of the same bot. For each pair, I then combine the programs using “two point crossover”. (Actually, I only do this 90% of the time; the other 10% of the time I just copy the original programs.) These two points are chosen randomly for each pair, and correspond to command numbers.
Simplifying it a bit, suppose that there were only 10 commands per program, and that I chose 3 and 7 as the crossover points. The programs would then look like this:
| Command | Parent 1 | Parent 2 | Child 1 | Child 2 |
|---|---|---|---|---|
| 1 | Up | Down | Up | Down |
| 2 | Up | Down | Up | Down |
| 3 | Up | Down | Down | Up |
| 4 | Up | Down | Down | Up |
| 5 | Up | Down | Down | Up |
| 6 | Up | Down | Down | Up |
| 7 | Up | Down | Down | Up |
| 8 | Up | Down | Up | Down |
| 9 | Up | Down | Up | Down |
| 10 | Up | Down | Up | Down |
(It’s actually all 0-based rather than 1-based, but I’ve adapted it here for squishy meatbag brains.)
So, there are two parents here: one keeps going up and one keeps going down. Their middle sections are then swapped around, so the offspring go up/down/up or down/up/down; each child inherits characteristics from both parents.
Once I’ve generated the offspring (by crossover or cloning), I mutate some of the “genes” (commands). This only happens 0.1% of the time, but when it happens I’ll chose a new command to replace whatever was already there. (There’s a 25% chance that it would be the same command again, so genes will only actually change 0.075% of the time.) This is a balancing act: I want to introduce new genetic material that might be useful, without destabilising the population (which would work against evolution).
When I’ve filled up the next generation, the whole process starts again: I run each new bot through the maze and give it a score. So, when does it stop? The significant point here is that I’m not waiting for the perfect solution; in this case, that would be a straight line with one bend to the left. Instead, I’m waiting for “convergence”.
I say that a particular gene has converged if it’s the same for 95% of the population. In this case, that means that 48 out of 50 bots need to do the same thing at that point in the program; for instance, if they all start by going up then the first gene has converged. The population has converged when all of the genes have converged. The bots won’t all be identical at that point, but they will have pretty similar programs.
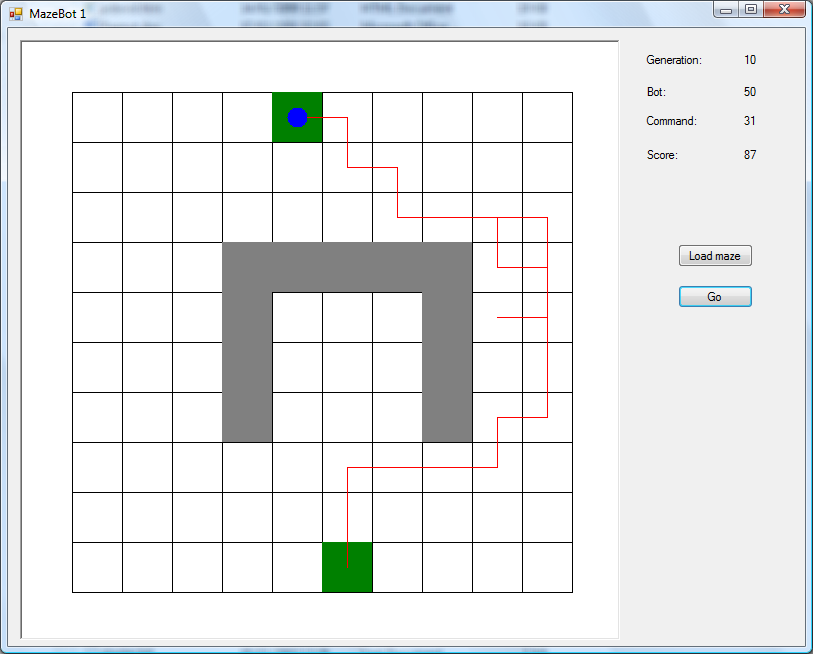
When the population has converged, I then pick the bot with the highest score. The whole process is non-deterministic (due to random numbers), i.e. I get slightly different results each time I run it, but here’s a typical winner:
This bot is obviously better than the one above; for one thing, it’s actually reached the exit! However, this still isn’t perfect: it doubles back on itself a couple of times, and isn’t following the shortest path towards the exit. I could keep running the program for further generations, but there’s not much point. To quote a line from Hitch: “You cannot use what you do not have.” In this case, that refers to genetic material; we know that at least 48 of the bots will move left as their second command, so we’re counting on the other 2 to do something better, which is (by definition) unlikely to happen. Looking at it another way, there’s no evolutionary pressure here; I’ve just found a bot that’s better than its local competition, rather than The Ultimate MazeBot.
As you can see by the top-right corner, it’s taken 21 generations to reach this point, so I’ve run 21 x 50 = 1050 bots through the maze. By contrast, suppose that I’d tried the exhaustive method, i.e. worked out every possible program and scored them all. There are 4 possible commands, and 100 commands per program, so that’s 4100 = 1.6 x 1060 possible programs! (I.e. that’s the phase space.) This is one of those ridiculous situations where you could run a billion bots per second, starting at the Big Bang, and you’d still only have scratched the surface. This is where genetic algorithms come in handy (at least in theory): you can get a “good enough” solution in a reasonable amount of time.
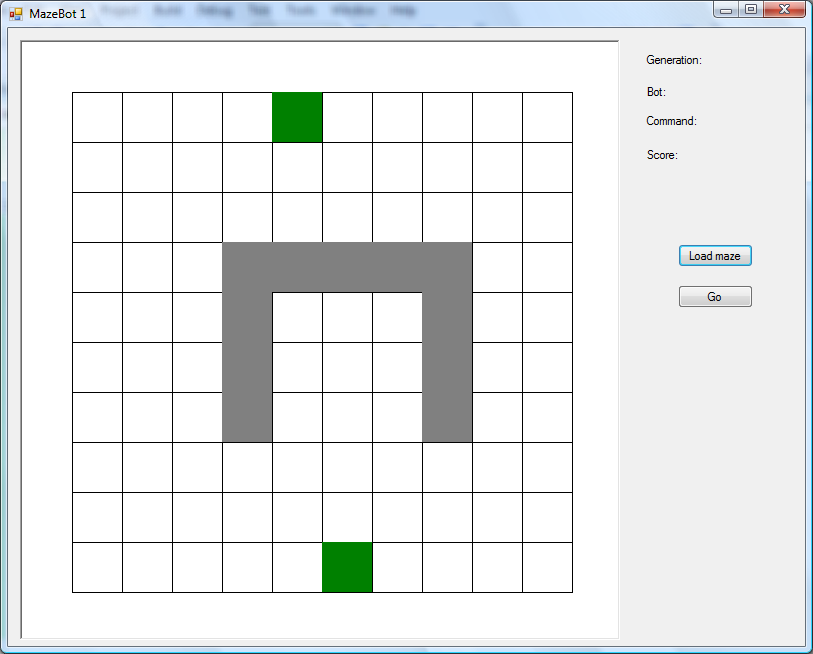
So, if it works in an empty maze, how about something slightly more tricky?
This one has a U-shape in the middle, which works the same way as the outer edges of the maze, i.e. if a bot tries to move through it then it just wastes a move and stays put. I ran this through the generations, and got another winner:
As before, it’s not perfect (it goes a bit wonky on the right hand side), but the bits above and below the wall are pretty good.
So, what does this all mean? In one of Richard Dawkins’ books (The Blind Watchmaker, I think), he talks about his “biomorphs”. These are a form of artificial life, which draw patterns on the screen. By picking his favourites, he wound up with some biomorphs which resembled the letters of the alphabet, and he used this to demonstrate that evolution is feasible. However, some people objected to this on the grounds that he was acting as an “Intelligent Designer” himself. So, I’ve tried to be more objective here: I set up the ground rules, then left the program to run by itself without my interference.
I think I’ve demonstrated that something happens, but it’s not quite what I was going for. The population has converged every time I’ve run the application (i.e. my “outer” program as opposed to the bot programs), and the final bot has always had a pretty good score. On the other hand, I’ve also generated a successful bot in the first generation each time, so I could have just stuck with that and not bothered with evolution at all. In fact, there have been a few cases where the final bot is worse than the initial leader! Of course, this doesn’t prove anything about the evolution of animal/plant life, one way or the other.
There is scope for further development here. For instance, it may be that my program is too long; if I reduce it to 20 commands, that would still be enough to finish either of my simple mazes, but I wouldn’t expect to get a solution in the first generation. However, it might then be impossible for the bots to complete a more complex maze, which seems a little unfair on them! Since I already know the shortest path, that’s not a huge problem, but it would mean that I couldn’t use the bots to find the shortest path for me.
As a related issue, I stop moving a bot once it’s hit the exit, which I think is reasonable. However, that means that all the commands after that point are effectively junk, and doing crossover on them is a waste of time. One option is to introduce a “no op” command, i.e. “just sit still and do nothing”. Going back to The Blind Watchmaker, it reminds me of the experiment regarding sexual selection and the tail length of certain birds. (The basic idea being that females are attracted to males with long tails.) “If it is true that the actual tail length of males is a compromise between a utilitarian optimum on the one hand, and what females really want on the other, it should be possible to make a male super-attractive by giving him an extra long tail. This is where the superglue came in.” Dude!
In this context, it would be good to give bots an advantage if they do less work, assuming that corresponds to some (theoretical) reduction in resources. It would be better to modify the length of the program, which does occur in nature, but it’s a lot more complicated to code!
Another option is to follow the Robo Rally approach. So, rather than letting the bots move in any direction, change the commands so that they can turn left/right and move forward/back. This means that it would take more commands to move the same distance, e.g. “move forward, turn left, move forward” rather than “move forward, move left”.
Taking that further, I’d like to make the bots a bit more autonomous. At the moment, they’re effectively blind, so they just trundle around following their program. An alternative is to let them see what’s ahead of them, and react accordingly (rather than having a “birds eye” view of the maze). I’m sure that I could write a program with an optimal strategy quite easily, but that’s not the goal here. Instead, I’d like the bots to have several pieces of information available that can affect each decision, and then the goal is to work out which things are most significant. For instance, if there’s a wall straight ahead, it would be a bad idea to move forward into it, but if there’s a wall on the left then that shouldn’t affect the “move forward” decision. I’d see it working a bit like this:
| Move forward | Turn left | Turn right | |
|---|---|---|---|
| Wall ahead | 0.1 | 0.2 | 0.3 |
| Wall on left | 0.4 | 0.5 | 0.6 |
| Wall on right | 0.7 | 0.8 | 0.9 |
So, I’d fill up the table with random values, then set the bots rolling. Each time a bot moves, it would see which conditions apply, then add up the weightings for each one that does. It would repeat this for each possible command, then choose the command with the highest total. (Matrix multiplication would probably help there.) When each generation finishes, I’d be breeding the weightings together, rather than the actual commands.
With MazeBot 1 (intended to be the first version of many!), there’s no reason to think that a bot which does well in one maze will do particularly well in a different maze. In fact, it would probably do quite badly, due to hitting walls. On the other hand, a bot with sensible weightings should be able to use its experience in several different mazes. I’d like to keep my core “bot program” as simple as possible, so that most of the behaviour is dynamic. I’m thinking along the lines of Bayesian spam filters, where the bot could make its own associations. This would hopefully match the behaviour of lab rats in mazes, e.g. the bots could be “trained” (bred) to turn right whenever they encounter a red square.
There are other changes I can make to the fundamental techniques. For instance, bots are essentially immortal, so there’s no reason that they have to be replaced by their offspring; I could keep the top 25 from one generation and just breed 25 new ones. I could also fine tune the intermediate population, since it may be too heavily weighted in favour of high scorers at the moment. For instance, I could put bots into bands, and say that the top 5 bots get 10 copies each, rather than doing a steady progression. That might turn out to be worse, but it would be useful to test. Thinking back to a book I read (about doing a PhD), if I design the experiment properly then there should be no such thing as a bad result, because whatever happens I’ll learn something new.
Having said all that, I have to admit that there’s nothing really groundbreaking here. For instance, I found a similar task being given out as a homework assignment. This also doesn’t count as rigorous science: I really ought to gather more information in each generation, e.g. seeing whether the scores fall into a bell curve distribution. Still, it’s nice to do some “garage band science” (borrowing a phrase from Levy), as a change from my normal work.